Research

Low-Complexity Constraint Differential Inverse Kinematics

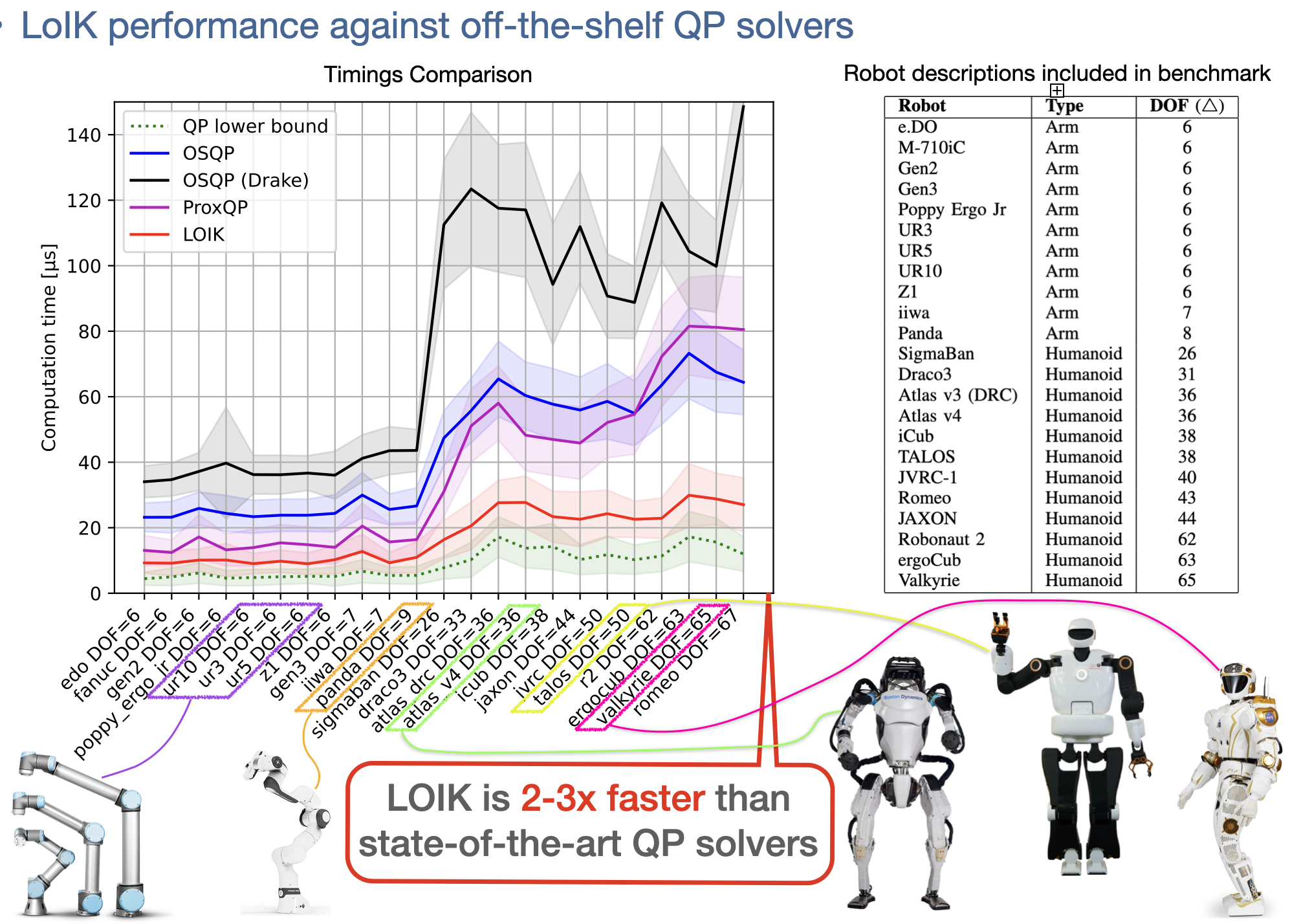
I introduced a novel constrained differential inverse kinematics solver that reframes the problem from an Augmented Lagrangian perspective. The resulting solver, LoIK, achieves linear-time complexity in both the total degrees-of-freedom of the robot, and the number of constraints in the problem. The low time-complexity makes it suitable for real-time control and planning of complex systems like humanoid robots with multiple equality/inequality constraints. As shown in the benchmarks, LoIK consistently outperforms the state-of-the-art, general-purpose quadratic programming solvers. This work was published in Robotics: Science and Systems (RSS) 2024. Pre-print available here. The open-source solver is available on GitHub.

Agile Quadruped Jumping Through Full-Centroidal-Momentum Model Predictive Control

I designed a real-time convex model predictive controller (MPC) for dynamic quadruped jumping, utilizing the full-centroidal-dynamics model, via the centroidal-momentum matrix. The designed controller is capable of correcting reference trajectory in real time, and is robust enough to be directly deployed on hardware without any additional low-level whole-body controllers. Hardware experiments for continuous 90-degree jump-turns are conducted on the MIT mini-cheetah platform. This work is published at the IEEE Robotics and Automation Letters (RA-L). Pre-print available here.

Momentum-Aware Planning Synthesis for Dynamic Legged Locomotion

I developed a bi-level trajectory optimization framework for generating dynamic and agile motion for quadruped robots. The proposed framework consists of two optimization components: a centroidal optimization using reduced order centroidal dynamics with linear and angular momentum as decision variables; and a whole-body-dynamics-based differential-dynamic-programming optimization. Consensus constraints are enforced to drive convergence between the two components. Below are sample trajectories generated using the proposed framework for the quadruped A1, to perform high-speed trotting, zero-gravity body re-orientation, and jump-turns.

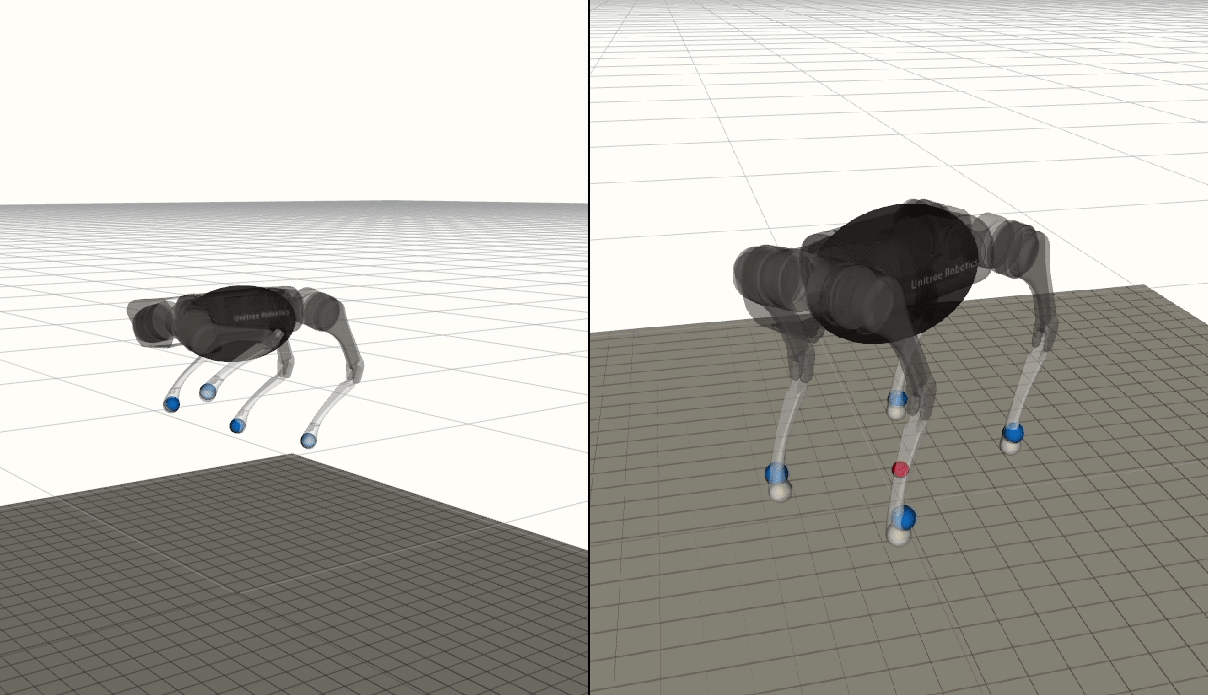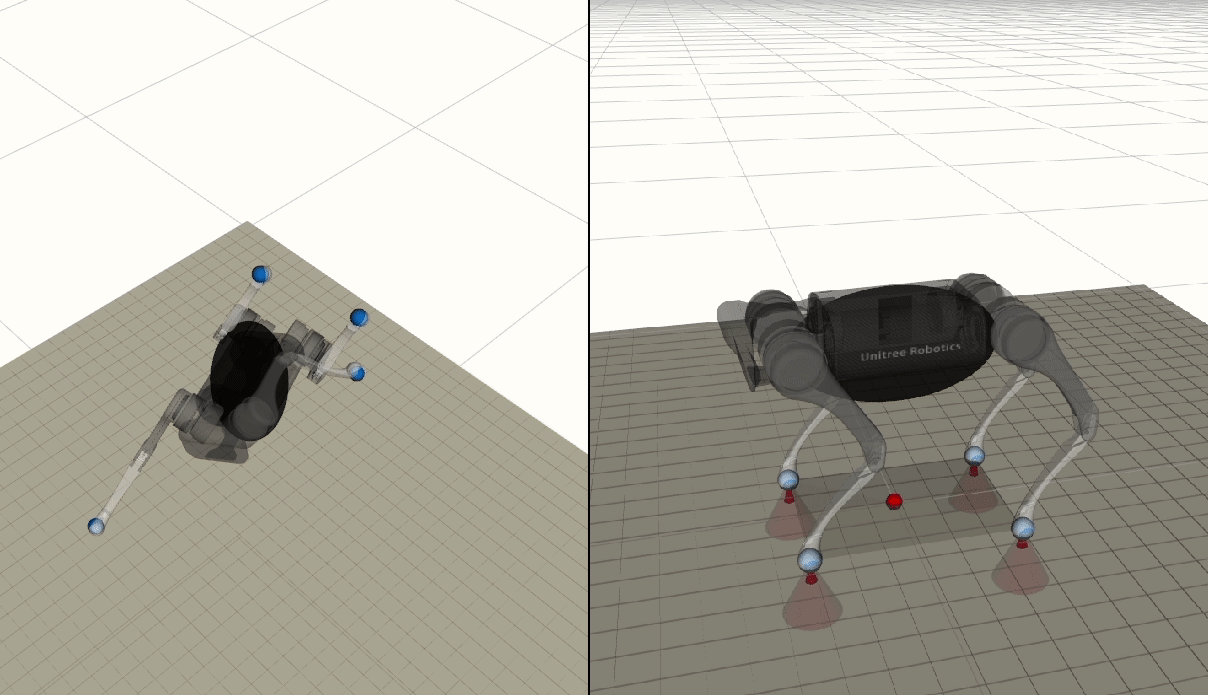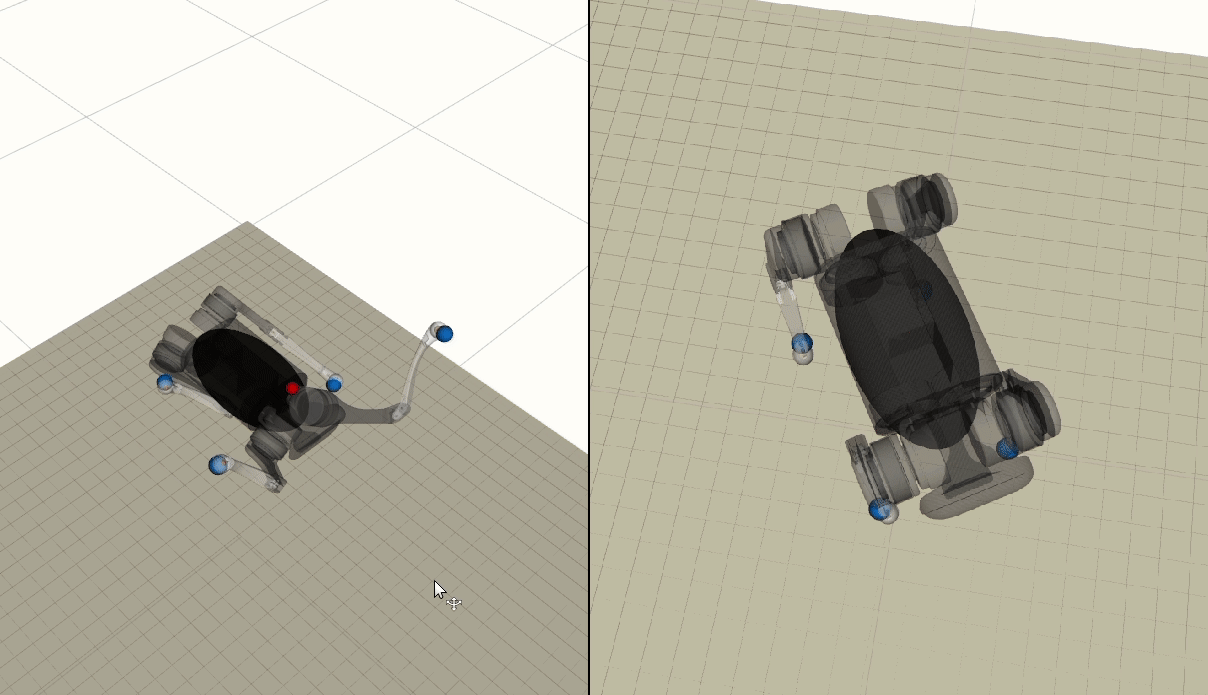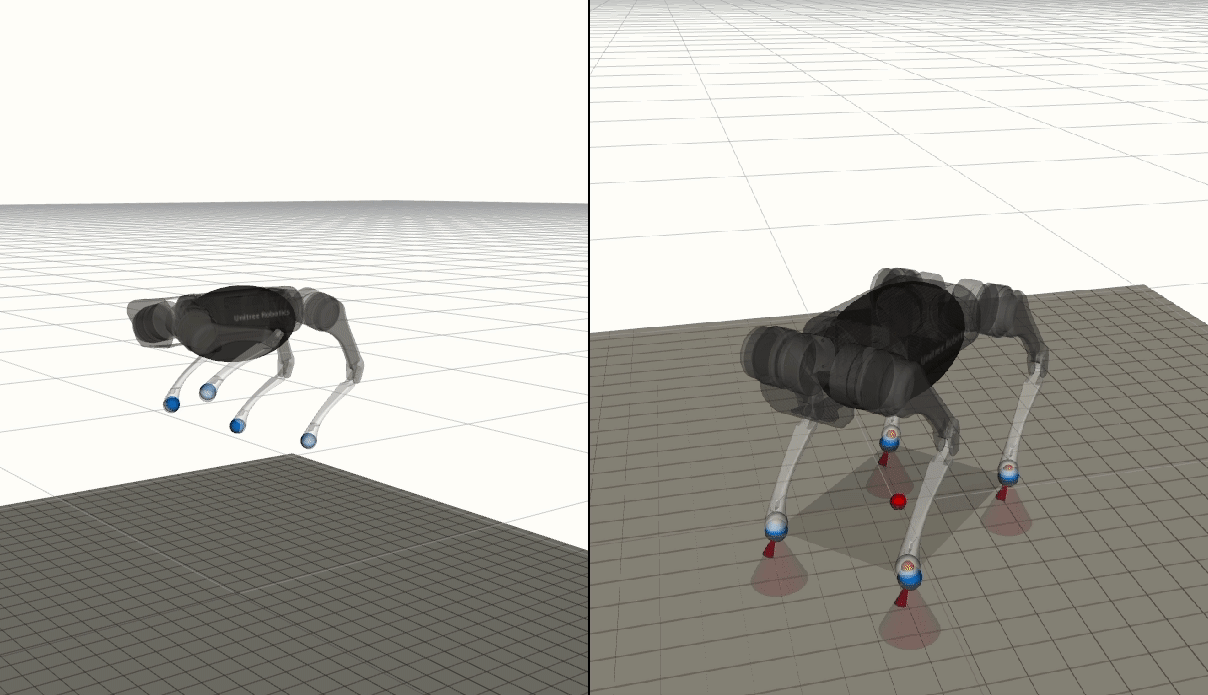
Extending Riemannian Motion Policies to Underactuated Wheeled-Inverted-Pendulum Robots

For this project, I developed a reactive policy motion planning pipeline for wheeled-inverted-pendulum based humanoids. A dynamics decomposition technique is proposed to split the full dynamics of the robot into fully actuated and underactuated subsystems. Leveraging Riemannian motion policies and differential-dynamic-programming, one can independently plan trajectories for fully actuated and underactuated dynamics, which are then combined into a single motion plan through null-space projection. This work is published at ICRA 2020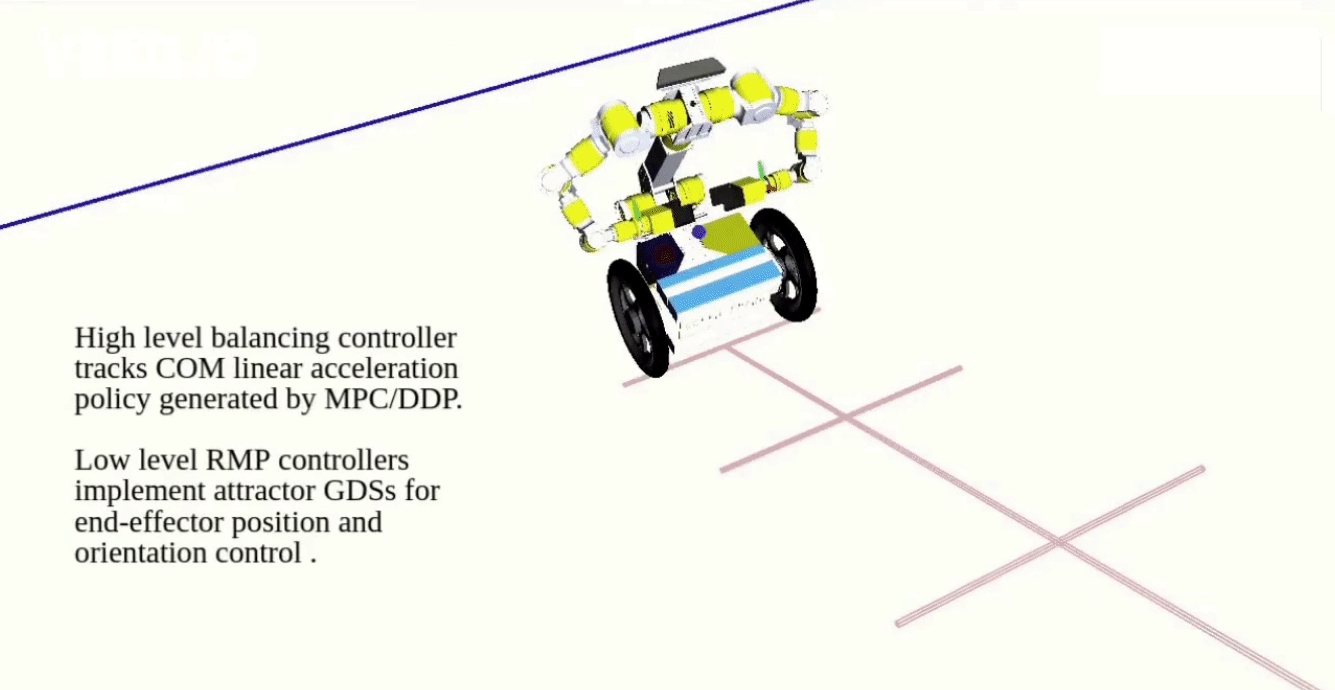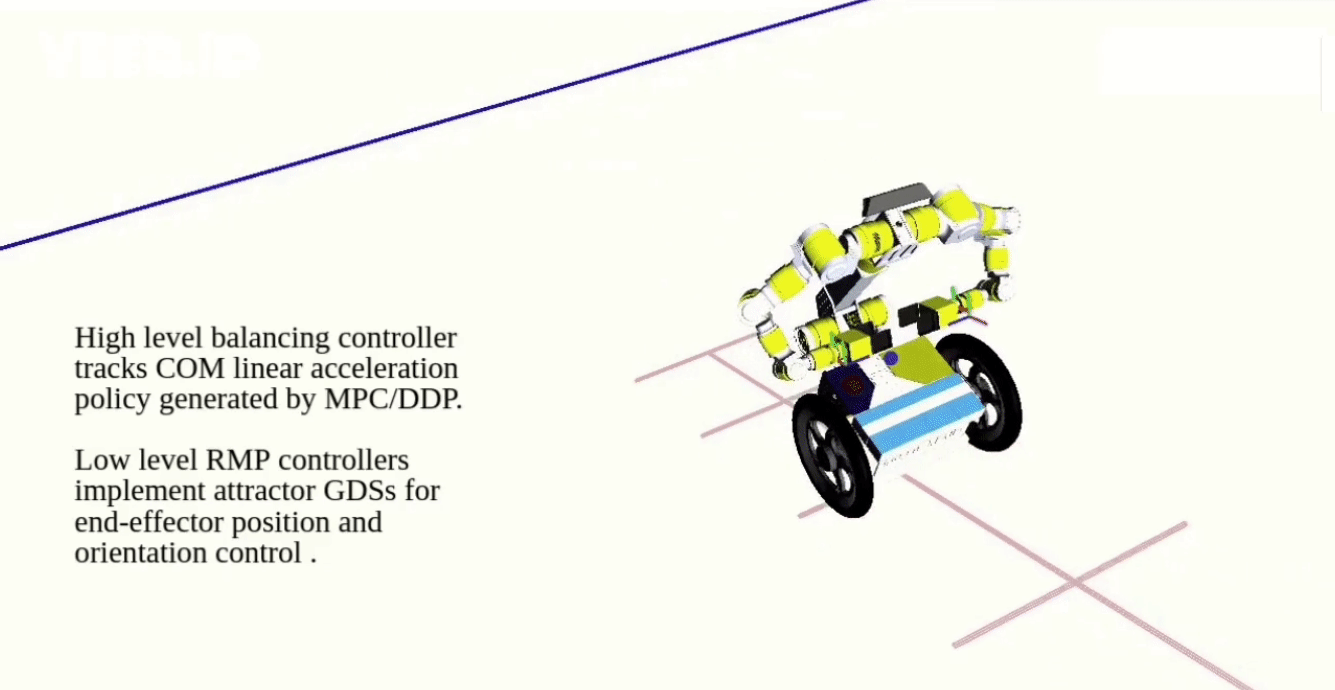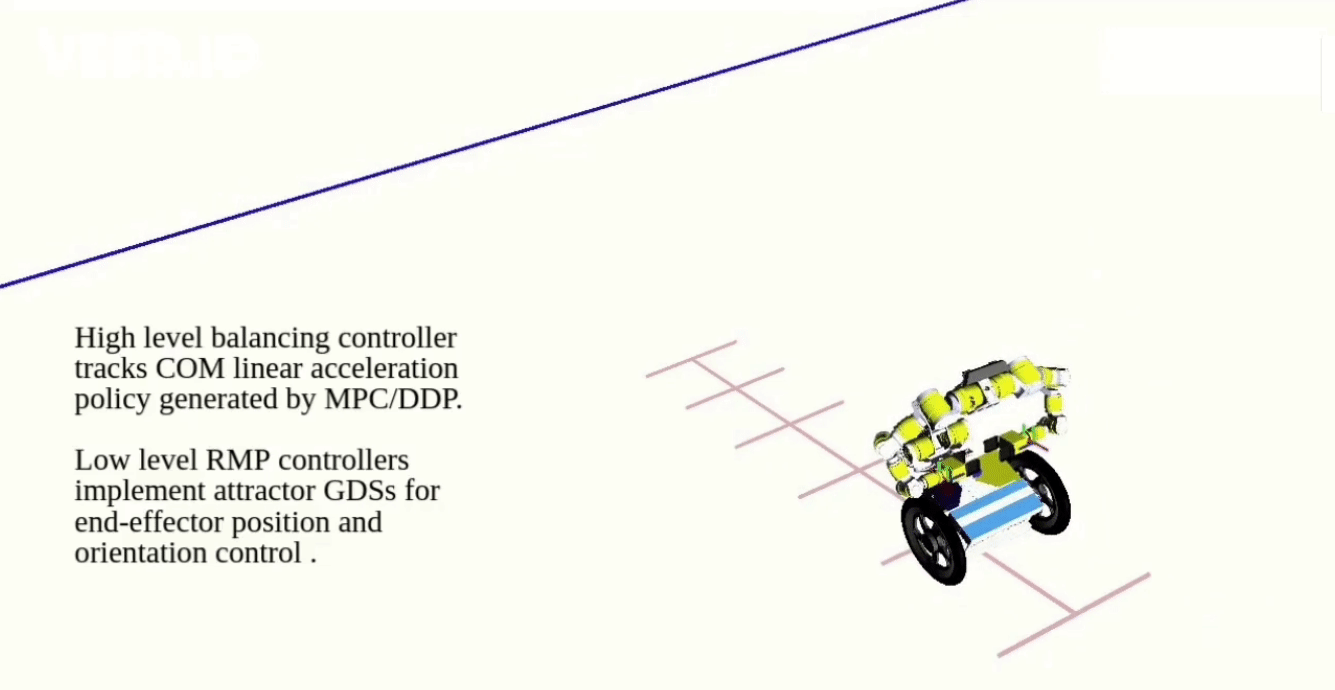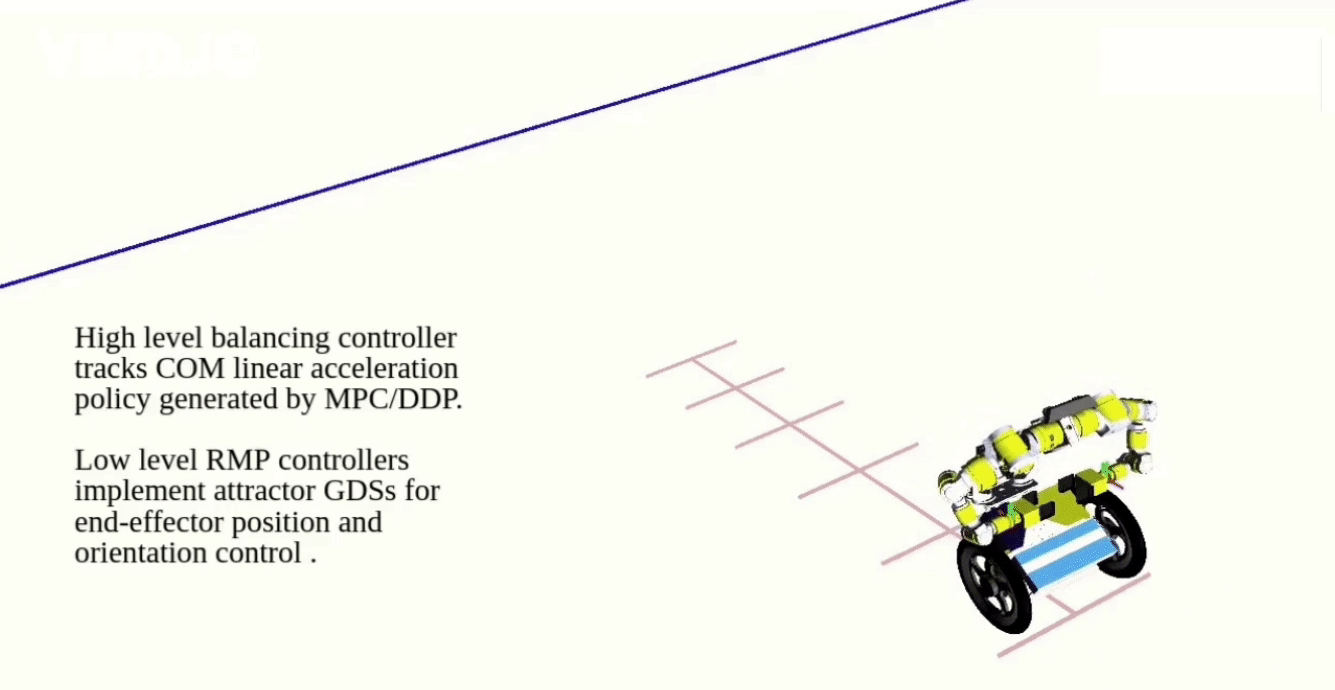

Adaptively Robust Control Policy Synthesis Through Riemannian Motion Policies

In this project, I proposed a robust control-Lyapunov-function (CLF)-based tracking controller, capable of handling large magnitudes of dynamic uncertainty and external disturbances. Additionally, I devised an automatic robust gain scheduling procedure that guarantees the stability and boundedness of the proposed controller. Experimental result on the KUKA iiwa manipulator platform is demonstrated below, for object tracking and obstacle avoidance tasks. This work is published at Control Systems Letters 2021

Distributed Optimal Control Framework based on Coordinate Descent Optimization for Multi-Agent Robots

In this paper, I helped develop a distributed optimal control framework for a multi-agent robotics system based on coordinate-descent optimization. The proposed framework exploits the underlying graph topology to compute the optimal control trajectory in a distributed manner. The proposed algorithm is then tested on a problem where a team of robots is tasked with establishing a communication link between source and destination while minimizing the overall system mobility and communication energy cost. Here is a sample of our algorithm running on the Gatech Robotarium platform using a cluster of 8 mobile robots. This work is published at CASE 2021